感度,特異度,尤度比を理解しよう!【JJCLIP#6】検査陰性なのにインフルエンザ?
2019
6/29
当ページのリンクには広告が含まれています。
※当ブログはアフィリエイト広告を利用しており,記事にアフィリエイトリンクを含むことがございます
感度,特異度,尤度比ゆうどひ って何ですか?
感度 ( Sensitivity ) とは,疾患ありのうち,検査陽性 特異度 ( Specificity ) とは,疾患なしのうち,検査陰性 尤度比ゆうどひ ( Likelihood ratio ) とは,英語でいえば,Likelihood ratio と表現するもので,「尤」は「もっとも👉尤も」と書く。つまり尤度比とはもっともらしさ,「~っぽさ」を表す用語である
感度や特異度は以下の表で理解しよう
疾患あり 疾患なし 合計
検査陽性 a人
b人
a+b人
検査陰性 c人
d人
c+d人
合計
a+c人
b+d人
a+b+c+d人
JJCLIP#6 検査で陰性なのにインフルエンザって?
この記事は,2014年2月16日(日)のJJCLIP配信 の内容を元にして作成しました。
ツイキャス では,検査キットによる診断精度の論文をもとに,感度,特異度,尤度比ゆうどひ といったものからベイズの定理まで話が展開 されます。非常に興味深い内容であると共に,知っておきたい用語がたくさん出てきたので備忘録として記録しています。
目次
検査で陰性だったのにインフルエンザと診断された! ~ツイキャス仮想シナリオ~
あなたは保険薬局の薬剤師です。インフルエンザが流行期を迎え,あなたの地域にはインフルエンザ流行警報がでています。
朝からインフルエンザと思われる患者さんばかりで,夜の6時を回っても途切れる気配がありません。
そこに一人の患者さんが浮かない顔をして処方箋を持ってこられました。
「今日は,ものすごく混んでて,先生によく確認できなかったんですが,腑に落ちないことが多くてちょっと伺っても良いですか?」
「まず,先生は“インフルエンザの検査はしなくても,あなたはインフルエンザだと思います。”とおっしゃって,心配なんで,どうしても検査してほしい,って頼んだんです。結果は陰性だったんで,安心したんですが,先生はそれでも“インフルエンザだろう”っておっしゃるんです。“薬いらないと思いますけど,どうします?”って聞かれたんですけど,インフルエンザだったらやっぱり飲んだほうが良いかなって思って,とりあえず,“じゃ,ください”って言って,今日はこの薬が出たんですけど…。インフルエンザの検査はしなくて良いってどういう事ですかね。それと陰性でもインフルエンザです,ってどういう意味でしょうか。よくわからないのですが,私は本当にインフルエンザなのでしょうか?」
この患者さんの主な情報と主訴は以下の通りです。
*30歳女性。喫煙(-)。電車通勤で都内まで勤務。
*今日の10時くらいから症状が出始めた
*症状は,主に発熱(39度)と寒気,関節の違和感
*合併症や併用薬なし。今日の処方はタミフル®とカロナール®
*インフルエンザの検査はしなくても良いってどういうこと?
*結局のところ,私はインフルエンザなのでしょうか?
インフルエンザ迅速診断キット検査の性能について少し調べてみました。
PubMedのClinical Queriesに「rapid influenza antigen detection test」とキーワードを入れ,カテゴリーを「Diagnosis」スコープを「Narrow」にして検索すると以下の論文が見つかりました。
[文献]
Tanei M, Yokokawa H, Murai K, Sakamoto R, Amari Y, Boku S, Inui A, Fujibayashi K, Uehara Y, Isonuma H, Kikuchi K, Naito T.
PMID: 24384898
http://blog.hidexp.net/?eid=327 より引用
横断研究について
横断研究と言うのは時間軸の無い,その時点(仮想シナリオでいえば,女性患者さんが受診した日)でスパッと切ったStudyのこと。
診断であれば,その時点で患者さんが病気を持っているのか否かを診れればいいので,時間的な因果関係というよりはその時点での有病率を判断する のに適している研究 。
診断の横断研究論文,確認ポイントは7つ
研究デザインは何か? 標準検査は妥当か? Gold standard に近いもので比較されているか。対象患者は臨床上,適切な患者であるか? 研究で行われた診断法と標準検査は全ての患者で行われているか? 研究で行われた診断法と標準検査は独立して判定されているか? 研究で行われた診断法と標準検査の判定方法は明確か? 研究で行われた診断法と標準検査はいずれも再現性があるか?
今回の横断研究論文について,実際に確認ポイントをチェックしてみる
研究デザインは何か? 👉 横断研究である。論文タイトルにズバリ書かれている標準検査は妥当か? 👉 妥当である。 論文アブストラクトのMain outcome measuresに記載あり。The RIADT and …(Verigene Respiratory Virus Plus; VRV) , … the gold standard , と記載あり。 「Gold standard(最も良い検査法)」という言葉と同じ意味で,しばしば論文では「Refernce standard キーワードとして覚えておくと良い☆対象患者は臨床上,適切な患者であるか? 👉 全く症状のない人を対象にしていると検査はほぼ確実に陰性が出るし,陽性が出てもそれは間違いなのは明らか。インフルエンザなのかどうか判別を必要とする患者さんを対象としているかどうかを書かれている部分を探すのが大事。論文ではアブストラクトのParticipantsに”upper respiratory symptoms and fever ≥37°C at any time from symptom onset”と記載あり。よってOK!研究で行われた診断法と標準検査は全ての患者で行われているか? 👉 methodsの中に”All were tested”と書かれている。全例で行われている。 OK!研究で行われた診断法と標準検査は独立して判定されているか? 一方の診断結果を知ったうえで,他方の診断を行うと情報バイアスが生じる。 👉 methodsの中に”participants were enrolled in the Departments of General Medicine of Juntendo University Hospital and Juntendo University Nerima Hospital, both in Tokyo, Japan. ”とあり,独立性があるかは微妙なラインだが,ある程度保たれているかも。研究で行われた診断法と標準検査の判定方法は明確か? 👉 明確である。迅速キットの結果は明確に出るので明確と考えていいだろう。表研究で行われた診断法と標準検査はいずれも再現性があるか? 👉 検査キットを使わないものであれば医師の手技が入るので個人差が出るので結果の一致が困難な場合があるが,今回のインフルエンザの迅速キットの場合は手技レベルに差は出ないと思われる。また,本文中のRapid influenza antigen detection testにもoutpatient physicians and residents who had been well trained in the technique.と書かれている。なのでOK!
四分割表について
疾患の有無と検査陽性・陰性を四分割表にまとめて書き込みます。
実際に論文に合わせて計算することで理解しやすくなるので,読み進めていってな☆
四分割表の書き方
書き方の覚え方やで
疾患の有り無しは神のみぞ知るので上に書く(上の”行”に並べて書く)。そして神は上から下を見るので縦に表を見る
検査の陽性か陰性か?は人間がやるもの。人間は神様より下にいる(地上にいる)ので下に書く(下の”列”に並べて書く)。そして人間は地上にいて,横に表を見る。
そんな風に覚えると四分割表づくりは正しく書ける☆
四分割表はこんな感じや
疾患あり 疾患なし 合計
検査陽性 a人
b人
a+b人
検査陰性 c人
d人
c+d人
合計
a+c人
b+d人
a+b+c+d人
今回の論文の結果を書き込んでいきます。
数値を書き込むと,わかりやすい!
疾患あり 疾患なし 合計
検査陽性 43人
2人
45人
検査陰性 16人
21人
37人
合計
59人
23人
82人
けいしゅけ
色々な場面で使えるので,四分割表は覚えておくとええで☆
[/ふきだし]
【四分割表から求められる7つのこと】尤度比ゆうどひ ・陰性尤度比ゆうどひ
けいしゅけ
さあ,ここからが超重要や!!
[/ふきだし]
7つの用語を解説します!
有病割合 感度Sn 特異度Sp 陽性的中率PPV 陰性的中率NPV 陽性尤度比ゆうどひ 陰性 尤度比 ゆうどひ
タコちゅけ
順番に行きまちゅよ~☆
[/ふきだし]
1. 有病割合って何ですか?
研究参加全体における疾患保有者の割合のこと。 四分割表で計算する場合 a+c / a+b+c+d で計算できる。
今回の論文の場合は 59 / 82 ≒ 0.719 👉 72 %
2. 感度Snって何ですか?
疾患ありのうち,検査陽性 四分割表で計算する場合 Sn = a / a+c で計算できる。
今回の論文の場合は43 / 59 ≒ 0.7288 👉 72.9 %
αエラーも教えてください
αエラーは”あわてんぼうのα”と呼ばれる。つまり,実際には疾患がないにもかかわらず,検査陽性
四分割表で計算する場合, b / b + d で計算できる。または α = 1 – Sp
今回の論文の場合は2 / 23 ≒ 0.087 もしくは,1 – 0.913 = 0.087 👉 8.7 %
3. 特異度Spって何ですか?
疾患なしのうち,検査陰性
今回の論文の場合は 21 / 23 ≒ 0.913 👉 91.3 %
βエラーも教えてください
βエラーは”ぼんやりβ”と呼ばれる。つまり,実際には疾患があるにもかかわらず,検査陰性
四分割表で計算する場合,c / a + c で計算できる。また,β = 1 – Sn
今回の論文の場合は 16 / 59 ≒ 0.271 もしくは, 1 – 0.729 = 0.271 👉 27 %
注意やっ!
感度と特異度は変化しない数値である!四分割表の縦に計算するものは,検査の時期によらず不変と覚えよう 疾患があるか,ないかという絶対数はインフルエンザであれば季節によって変化するものの,これらを検出する計算の割合は変わらないのだ。
4. 陽性的中率PPVって何ですか?
診断結果が陽性 ある 四分割表で計算する場合 PPV = a / a+b で計算できる。
今回の論文の場合は 43 / 45≒ 0.9555 👉 95.5%
5. 陰性的中率NPVって何ですか?
診断結果が陰性 ない 四分割表で計算する場合 NPV = d / c+d で計算できる。
今回の論文の場合は 21 / 37 ≒ 0.5675 👉 56.8%
注意やっ!
陽性的中率と陰性的中率は変化する!四分割表の横に計算するものは,検査をする時期によって変わる!!! 例えばインフルエンザの検査を夏場に行った場合には,陽性的中率は下がるし陰性的中率は上がる。つまり,これらの数値は状況によって数値が変化するものなのだ!
6. 陽性尤度比ゆうどひ って何ですか?
実際に病気の人が,健常な人よりも何倍陽性
四分割表で計算する場合 ( a / ( a + c ) ) / ( (1 – d ) / ( c + d ) ) = Sn / 1 – Sp = (1 – β ) / α
今回の論文の場合は0.7288 / ( 1 – 0.913 ) ≒ 8.377
尤度比ってなんですか?
尤度比とは「~っぽさ」のこと
尤度比は英語でLikelihood ratio と表現し,LRと表記する。
LR = 病気を持つ人が所見を示す可能性 ÷ 病気を持たない人が所見を示す可能性参考:J Gen Intern Med. 2002 Aug;17(8):646-9. PMID: 12213147
「尤」は「もっとも👉尤も」と書き,
尤度比とはもっともらしさ,「~っぽさ」を表すわけや。
7. 陰性尤度比ゆうどひ って何ですか?
実際に病気の人が,健常者に比べて何倍陰性
四分割表で計算する場合 ( ( 1 – a ) / ( a + c ) ) / (d / ( c + d )) = 1 – Sn / Sp = β / ( 1 – α )
今回の論文の場合は( 1 – 0.7288 ) / 0.913 ≒ 0.297
事前オッズ × 尤度比 = 事後オッズの理解の仕方 検査前オッズに尤度比を乗じると検査後のオッズが算出できる(ベイズの定理)。
事前オッズ × 尤度比 = 事後オッズ
検査をする前は疾患があるかどうかがわからない。50%だ!と主観的に見積もる(検査前のオッズ)
これに,尤度比をかけることで(検査をすることで),
どのくらいの確率で「疾患ありだろう」と計算できる(検査後オッズ)
オッズと確率の違いとは?
オッズ,オッズとは言うけれど,オッズと確率の違いって何でしょうか??
〜[補足:確率とオッズは髪の毛の分け方でイメージせよ!]〜
ちなみにオッズ比と確率の違いを整理しておきます。
確率 ▶ ある事象/全体の事象
オッズ ▶ ある事象/そうでない事象
例えば,3人のうち1人がインフルエンザ,確率▶1/3,オッズ▶1/2
■確率が1/2⇒頭の真ん中で髪の毛を分けている⇒オッズ1/1
(中わけ:確率=5/5+5,オッズ=5/5)
■確率が3/10⇒髪の毛の七三分け!⇒オッズ3/7!
(七三分け:確率=3/7+3,オッズ3/7)
■確率が1/100⇒髪の毛はほとんど横にペタッとなっている!⇒オッズ1/99
(バーコード的:確率=1/99+1,オッズ1/99)
第6回薬剤師のジャーナルクラブの開催のお知らせ より引用
あまりにも青島先生のブログ記事でまとめられているものが分かりやすすぎるので引用にて。
僕は髪の毛の分け方のイメージをイラストで説明しようと思います☆
イラストはふざけています。でも,真面目にやってます!!
1:9はバーコード
5:5は真ん中分け
3:7は七三分け
SnNout:a sensitibe test,when Negative rules out disease と SpPin:a specific test , when Positive rules in disease
SnNout:a sensitibe test,when Negative rules out diseaseの意味とは?
感度が高いと病気の見逃し率が減る。所見がなければその疾患を除外できる可能性が高くなる という事。
SpPin:a specific test , when Positive , rules in diseaseの意味とは?
特異度が高いと,間違って病気と診断する確率が減り,所見があれば確定診断できる可能性が高くなる という事。
ややこしい!けいしゅけがミニ丸先生から教えてもらった検査の感度・特異度の考え方☆
この感度と特異度,感度が高くて特異度が低い場合は?とか,感度が低くて特異度が高い場合は?とか考えると頭がこんがらがってくるねんね。
なので,EBMerの先輩薬剤師,ミニ丸先生 に教えていただいた覚え方を記録しておこうと思う。備忘録として。
感度が高いのに,特異度が低い検査は・・・
検挙率が高いけど,濡れ衣だったり別の事件の犯人を捕まえる刑事みたいなもの
感度が低いが,特異度が高い検査は・・・
検挙率が低くて事件を迷宮入りさせやすいけど,捕まえる容疑者は真犯人である可能性は高い刑事みたいなもの
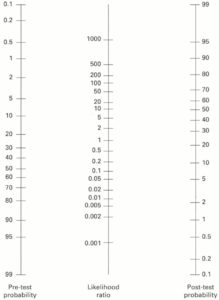
ベイズの定理からの,Faganのノモグラム!これを使えば事前確率から事後確率がわかる!
Fagan ノモグラム
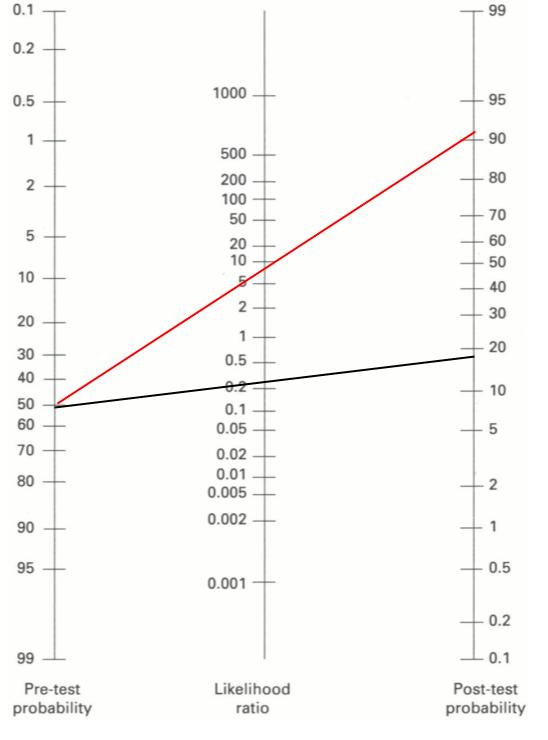
Faganのノモグラムに今回の陽性尤度比と陰性尤度比をプロットしてみます。(事前オッズは50%としました。)
Fagan ノモグラム 今回の論文の結果をプロットした
こうすると,陽性尤度比が8.4の検査だったので,事後オッズは 92 %になることがわかるねん。(まぁ,インフルエンザって言うて問題ないやろねってなる)
さらに,陰性尤度比が 0.3 の検査だったので,事後オッズは 18 %ほどということ。(この場合,実際にインフルエンザの患者さんでも20%近く偽陰性が出るやん!ってことになる。5人に1人は実は陽性でした・・・って笑われへんよね💦)
たこちゅけ
なるほどでちゅ☆
でも先生,陽性尤度比や陰性尤度比を計算できたとしてもノモグラフが手元になかったらどうしたら良いんでしょう?
単純に計算だけで大雑把になんとかならないものでしゅか?
[/ふきだし]
ノモグラフすら使わない簡易版の計算方法!
尤度比の単純化
尤度比
確率変化(概算)
疾患ありに対する
10
+45
かなり高くなる
9
8
+40
7
6
+35
5
+30
けっこう高くなる
4
+25
3
+20
2
+15
少し高くなる
1
0
なし
0.5
-15
少し低くなる
0.4
-20
0.3
-25
0.2
-30
けっこう低くなる
0.1
-45
かなり低くなる
(J Gen Intern Med. 2002 Aug;17(8):646-9. PMID: 12213147 を参考にして筆者作成)
この表があれば,ざっくりと計算は可能になるわ。
例えば,論文の場合は感度72.9%,特異度91.3%やった。
陽性尤度比が8.4なので,上の表から読み取って+40すると感度は100%を超える。
陰性尤度比が0.3なので,上の表から読み取って-25すると特異度が66%くらいになる。
タコちゅけ
特異度が66%の見積もり…。つまり,本当は病気じゃなくて検査結果も陰性となる確率が66%くらいってことでちゅよね。・・・あ,34%で実際は疾患があるのに陰性が出てしまう可能性が!!
[/ふきだし]
けいしゅけ
鋭いっ!!
そのとおり。そやから,仮想シナリオのドクターは検査結果が陰性であったにもかかわらずインフルエンザの薬を出したんやね。
[/ふきだし]
ちなみにインフルエンザと診断するための身体所見のシステマティックレビューもあります!
J Am Board Fam Pract. 2004 Jan-Feb;17(1):1-5.
A systematic review of the history and physical examination to diagnose influenza .
Ebell MH1 , White LL, Casault T.
PMID: 15014046
こういった論文もあるので読んでみると面白いと思います☆
このシナリオのまとめ。患者さんにはどう伝える??
検査が陰性でもインフルエンザとは言い切れないという事が分かりました。
薬剤師としてどう伝えましょうか?
「インフルエンザ検査の結果が陽性であれば,確実にインフルエンザであると言えます。ただ,陰性であった今回の場合はインフルエンザではないとは言い切れないんです。
インフルエンザ検査キットはインフルエンザであっても陰性と出ることもあるので,それで先生はインフルエンザのお薬を出されたのだと思いますよ☆」
こんな風にお伝えしてみたらいいのかもしれません。
[kjk_temp id=”5491″]
この記事が気に入ったら
 けいしゅけ
けいしゅけ




















記事の感想など,ひとこと頂けますか?