医療論文で見る統計用語【ITT（ Intention to treat ）解析】って何ですか？

ランダム化比較試験の統計解析対象集団についての用語を理解する

今回のテーマは統計解析対象集団に関する用語の解説です。

ぼく自身が，きちんと頭の中を整理するためにもできる限りシンプルにまとめていきたいと思います。

ランダム化臨床試験の解析対象集団はITTとFAS，PPSに分けられる

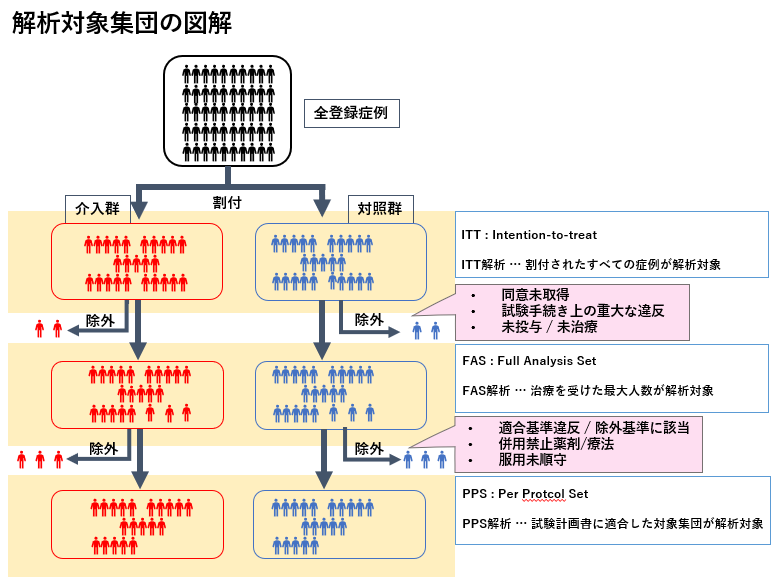
図解すると理解しやすいと思います。

ITT（Intention-to-treat）

ITT（Intention-to-treat）とは，母集団から割り付けられた全員を指します。最終的に試験終了の時には次の方々は実際には臨床試験を終了していません。

実際の治療でも，途中で受診をやめてしまう人や服薬アドヒアランスが悪い場合もありますよね。この解析対象集団はそういった人たちも考慮しているため実践に近いといえるでしょう。

ちなみに，脱落する人（治療をそもそも受けてない，受けたけれど効果判定できない人）を含めて評価判定するため，介入群に投与された薬剤と対照群に投与された薬剤（標準治療薬やプラセボ）の差は過小評価されます。逆に言えば，これで優位さが付いたとすれば，実践においてもしっかりと効果を表す治療である可能性が高いと言えます。

FAS（Full Analysis Set）

FAS（Full Analysis Set）とは，治療を受けた最大人数を指す解析対象集団です。とりあえず治療を受けた人が対象になっています。

PPS（Per Protcol Set）≒ｍITT解析

PPS（Per Protcol Set）は，試験計画書に適合した対象集団が解析対象になっています。治療薬とコントロールの効果の差に注目して結果を見たい場合には適していると言えます。しかし，試験計画書で適合基準や除外基準を変更することによって意図的に効果の差が出やすい集団を比べることにもなりえるため注意が必要です。

※mITT解析は、拡大した一種のper protocol解析

解析方法について触れていこうと思うけれども，その前にランダム化比較試験の「ランダム化」について触れておきたいかなぁと思っています。

ちなみに・・・ランダム化ってなんですか？

例えば1000人の患者さんを集めた臨床試験があるとします。実際に試験を開始する前に，

に分ける作業が行われるんやけど，500人ずつ分けるとして片方の群が男性ばかりでもう片方の群が女性ばかり・・・これではランダム（無作為）化されているとは言えないよね？

実際の医療の現場においては，一般的に（例外あり）

こういうものに関係なく薬は処方されます。（＊もちろん対象が限定される薬もあるけれど，ひとまずここでは深く突っ込まへんで☆）

なので，臨床試験もこれに近い状況になっている方が結果のデータが信頼できる。よって，臨床試験をするとなれば，集まった臨床試験を受ける人（被験者と言います）を老若男女，体型に偏りがないようにランダムに治療薬群とコントロール群に分けるわけですわ。

うん，理屈としてストンと通りますよね？

さて，臨床試験を開始し，試験を進めて行き，試験終了になる。

この流れの中で，必ずしも初めに集まった全員の被験者さんが臨床試験を終了できるわけではないねん。

こんなことがあって，当初1000人を集めて試験薬群500人，コントロール群500人にランダム化したのに，最終的に50人の脱落者が出て950人の参加者，試験薬群478人，コントロール群472人のランダム化になった

あらためてITT解析とPPSの違いについて話そう

ＩＴＴ解析ではプロトコール逸脱があってもそのまま解析をする

つまり，プロトコール逸脱者がいたとしても，1000人の患者さんを試験薬群500人，コントロール群500人という割り付け通りに解析をするわけや。

per protocol解析ではプロトコールを遵守できた人だけ（逸脱者を除いた人数のみ）で解析をする

一方で， per protocol解析では，先ほど挙げた例のように５０人のプロトコール逸脱が出た場合（試験薬群で22人，コントロール群で28人のプロトコール逸脱が出たと仮定します）に，

950人の患者を，試験薬群478人，コントロール群472人として解析をするねん。

ＩＴＴ解析の意義ってなんですか？良い点と悪い点を教えてください

答え：ＩＴＴ解析の最大のメリットは，ランダム化割り付けの担保がされることによって結果のデータが実臨床でのデータに近いということ。

ただし，治療効果が過小評価されるという欠点がある。

どういうことか？

こういった患者の数が大きくなればなるほど，解析にはそういった人の人数も母集団として計算に含まれるので試験データの結果が小さく出る。つまり，治療効果が過小評価されてしまうことになってしまうねん。

ただし，実際の医療現場においても服薬しない患者さんはいるし，服薬を中止する患者さんもいるから，ＩＴＴ解析の結果≒実臨床の結果ととらえることが出来る。

　アカン，ピンと来ぉへん！と言う方へ補足説明です

ＩＴＴ解析の説明，もうちょっとわかりやすくなりませんか？

どういうことかというとやなぁ，200人の学生を100人ずつ学習塾に通わせるＡ群と，通わせないＢ群に分けたとする。

結果としてどちらがある難関校への合格率が高いか？を解析する。なぁんて試験をするとしよう。ここで，学習塾に通わせるＡ群で20人の脱落があったとして，80人が塾に通い，20人は通わなかった。（Ａ群のアウトカム：塾に通った80人のうち，30人が難関校に合格し，通わなかった20人のうち2人が合格した）

学習塾に通わないＢ群で10人の脱落があり，90人が塾に通わず，10人は塾に通った。（Ｂ群のアウトカム：通わなかった90人のうち7人が合格し，塾に通った10人のうち，3人が難関校に合格した）

こうなったときを例にすると理解しやすいんや。

もしもＡ群で塾に通わなかった人数（プロトコル脱落）を加味すると，はじめにランダム化でＡ群に割り付けられたうち，さらにその中でも塾にちゃんと通った人の合格率を見ることになる。

Ｂ群で塾に通った人数（プロトコル脱落）を加味すると，はじめにランダム化でＢ群に割り付けられたうち，さらにその中でも塾にちゃんと（？）通わなかった人の合格率を見ることになる。

これって，はじめにランダム化した時と比べると割り付けられた人の背景が変わってしまっている（はじめは全員塾に通うか，通わないかで振り分けたはずやもの）！！！

ってことになるねんなぁ。

なので，当初割り付けた通りの100人ずつを解析するＩＴＴ解析はランダム化を担保する解析方法であることがわかるんや。

ＩＴＴ解析の結果が過小評価されるものの，実臨床に近い結果になる理由

先の表をもう一度見てみよう。

Ａ群の場合，全体での合格率は３２％やけど，

Ａ群で実際に塾に通った人の合格率を見ると３７．５％で

Ｂ群の場合，全体での合格率は１０％やけど，

Ｂ群で実際に塾に通わなかった人の合格率を見ると７．８％や。

つまり，プロトコル逸脱を加味した方が，振り分け条件に対する結果はハッキリと出るねん。

逆を言えば，これをプロトコル逸脱も含めてランダム化を担保するＩＴＴ解析の場合，結果が過小評価になっているとわかるよね☆

ただし，実生活においてもＩＴＴ解析の結果の方が現実に近いことは感覚的にも理解できるやんね？

塾に通うって言うててもサボることだってあるし，塾に通うのをやめることだってあるもの。

そういった人も含めてひとまず塾に通うとした群と通わないとした群の割り付けを変えずに結果をデータ化する方が実生活にそのまんま結果を当てはめても大きくずれがないってわけや。

---

けいしゅけイチオシ勉強サイト

---

今回の記事はここまでや☆

最後まで読んでくださってホンマおおきにっ！！お時間を使って読んでくださったことに心から感謝申し上げます！